🧠 Khám phá AI #4: Hồi quy trong Học có giám sát

Trong bài viết này, chúng ta sẽ đi sâu vào một trong những nhánh cơ bản của học có giám sát: hồi quy. Nếu bạn đã từng cố gắng dự đoán giá nhà, giá trị cổ phiếu, hoặc nhiệt độ ngày mai, bạn đang làm việc với hồi quy.

Hãy khám phá hồi quy là gì, nó hoạt động như thế nào, các loại thuật toán hồi quy, hàm mất mát, thước đo đánh giá, và các trường hợp sử dụng thực tế.

📐 Hồi quy là gì?

Hồi quy là một tác vụ học có giám sát trong đó biến mục tiêu là liên tục chứ không phải phân loại. Mô hình học mối quan hệ giữa các biến đầu vào (đặc trưng) và một đầu ra số.

Ngược lại với phân loại, nơi chúng ta dự đoán nhãn, trong hồi quy chúng ta dự đoán các số thực.

🏡 Ví dụ: Dự đoán giá nhà

Hãy tưởng tượng chúng ta muốn dự đoán giá của một ngôi nhà dựa trên các đặc trưng như:

Diện tích
Số phòng ngủ
Xếp hạng khu phố

Mỗi mẫu huấn luyện chứa cả đặc trưng (đầu vào) và giá bán thực tế (đầu ra). Mô hình học cách ánh xạ các kết hợp đặc trưng thành một giá trị mục tiêu liên tục.

🧠 Các thuật toán hồi quy phổ biến

Thuật toán	Mô tả	Phù hợp cho
Hồi quy tuyến tính	Mô hình hóa mối quan hệ tuyến tính giữa đặc trưng và đầu ra	Baseline nhanh, mô hình có thể giải thích
Hồi quy đa thức	Mở rộng hồi quy tuyến tính với các thuật ngữ đa thức	Xu hướng phi tuyến
Hồi quy Ridge / Lasso	Hồi quy tuyến tính với regularization để ngăn overfitting	Dữ liệu nhiều chiều
Hồi quy cây quyết định	Chia không gian đầu vào để giảm thiểu phương sai trong mỗi vùng	Mối quan hệ phi tuyến đơn giản
Hồi quy rừng ngẫu nhiên	Tập hợp các cây cho hồi quy mạnh mẽ	Dữ liệu dạng bảng với tương tác phức tạp
Mạng nơ-ron	Mô hình đa lớp với kích hoạt phi tuyến	Dữ liệu phức tạp, nhiều chiều (ví dụ: hình ảnh)

🧮 Hàm mất mát

Để đo lường mức độ tốt của dự đoán, chúng ta sử dụng hàm mất mát.

🔹 Sai số bình phương trung bình (MSE)

\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2

Phạt các lỗi lớn hơn mạnh hơn
Nhạy cảm với outliers

🔹 Sai số tuyệt đối trung bình (MAE)

\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|

Ít nhạy cảm với outliers hơn
Có thể giải thích hơn (cùng đơn vị với đầu ra)

🔹 Mất mát Huber

Kết hợp MSE và MAE; bậc hai cho lỗi nhỏ, tuyến tính cho lỗi lớn

📊 Thước đo đánh giá

Sau khi huấn luyện, chúng ta đánh giá mô hình hồi quy bằng:

Thước đo	Mô tả
Điểm R² (Hệ số xác định)	Đo lường tỷ lệ phương sai được giải thích bởi mô hình
RMSE (Căn bậc hai sai số bình phương)	Căn bậc hai của MSE; cùng đơn vị với đầu ra
MAE	Sai số tuyệt đối trung bình
MAPE	Sai số phần trăm tuyệt đối trung bình (dựa trên phần trăm)

Một mô hình hồi quy tốt nên tổng quát hóa tốt - lỗi thấp trên cả dữ liệu huấn luyện và xác thực.

🧪 Dự án thực hành: Dự đoán giá xe

Một tập dữ liệu mẫu có thể bao gồm:

Đặc trưng đầu vào: Tuổi, số km đã đi, thương hiệu, kích thước động cơ, loại nhiên liệu
Đầu ra mục tiêu: Giá bán tính bằng USD

Bạn có thể sử dụng scikit-learn để xây dựng:

Một mô hình LinearRegression
Đánh giá bằng mean_squared_error và r2_score
Trực quan hóa dự đoán so với thực tế

Mẹo: Luôn kiểm tra biểu đồ residual để đảm bảo mô hình của bạn không sai một cách có hệ thống.

✅ Khi nào sử dụng hồi quy

Sử dụng hồi quy khi:

Đầu ra của bạn là một số thực (ví dụ: giá, độ dài, nhiệt độ)
Bạn quan tâm đến độ lớn của lỗi
Mối quan hệ giữa đầu vào và đầu ra có thể là tuyến tính hoặc phi tuyến

❗ Những lỗi thường gặp

Overfitting với các mô hình phức tạp (đặc biệt trên tập dữ liệu nhỏ)
Bỏ qua outliers, có thể làm méo mô hình
Không chuẩn hóa hoặc tiền xử lý đặc trưng (đặc biệt với các mô hình dựa trên gradient)

🧪 Ví dụ mã: Hồi quy tuyến tính đơn giản trong Python

Chúng ta sẽ tạo một tập dữ liệu tổng hợp với mối quan hệ tuyến tính và huấn luyện một mô hình LinearRegression bằng scikit-learn.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split

# 🎯 Tạo dữ liệu tổng hợp
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)  # Mối quan hệ tuyến tính với nhiễu

# 🔀 Chia thành tập huấn luyện và kiểm tra
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 🧠 Huấn luyện mô hình hồi quy tuyến tính
model = LinearRegression()
model.fit(X_train, y_train)

# 📈 Đưa ra dự đoán
y_pred = model.predict(X_test)

# 📊 Đánh giá mô hình
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print(f"Sai số bình phương trung bình: {mse:.2f}")
print(f"Điểm R²: {r2:.2f}")
print(f"Tham số đã học: Intercept = {model.intercept_[0]:.2f}, Coefficient = {model.coef_[0][0]:.2f}")

# 📉 Vẽ kết quả
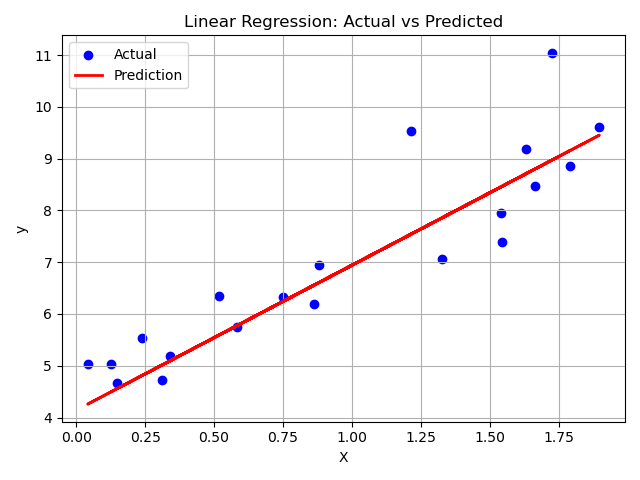
plt.scatter(X_test, y_test, color='blue', label='Thực tế')
plt.plot(X_test, y_pred, color='red', linewidth=2, label='Dự đoán')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Hồi quy tuyến tính: Thực tế vs Dự đoán')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

🔍 Biểu đồ dưới đây cho thấy một xu hướng tuyến tính rõ ràng: đường màu đỏ (giá trị dự đoán) chặt chẽ theo các chấm màu xanh (giá trị thực tế), cho thấy mô hình đã thành công trong việc nắm bắt mối quan hệ cơ bản mặc dù có một số nhiễu trong dữ liệu.

Biểu đồ hồi quy tuyến tính

🔚 Tóm tắt

Hồi quy là một công cụ cốt lõi trong hộp công cụ ML cho bất kỳ vấn đề nào liên quan đến dự đoán số. Bằng cách hiểu dữ liệu, chọn mô hình phù hợp, và đánh giá nó cẩn thận, bạn có thể xây dựng các hệ thống dự đoán đáng tin cậy cho tác động thực tế.

🔜 Tiếp theo

Tiếp theo trong loạt bài Khám phá AI: Phân loại - nơi chúng ta giải quyết vấn đề gán nhãn cho đầu vào như phát hiện thư rác, nhận diện hình ảnh, và chẩn đoán y tế.

Hãy tò mò và tiếp tục khám phá 👇

🙏 Lời cảm ơn

Cảm ơn ChatGPT đã cải thiện bài viết này với các gợi ý, định dạng và biểu tượng cảm xúc.