Published on

🧰 Vai trò của các hàm kích hoạt trong mạng nơ-ron

Authors

🧰 Vai trò của các hàm kích hoạt trong mạng nơ-ron

Các hàm kích hoạt là những anh hùng thầm lặng của học sâu. Không có chúng, mạng nơ-ron sẽ chỉ đơn giản là các ngăn xếp phép toán tuyến tính - bất kể sâu đến đâu. Trong bài viết này, chúng ta sẽ đi sâu vào cách hoạt động của các hàm kích hoạt, tại sao chúng cần thiết, và cách chọn đúng cho mô hình của bạn.

🔍 Tại sao chúng ta cần các hàm kích hoạt?

Hãy tưởng tượng một mạng nơ-ron không có hàm kích hoạt - nó chỉ là một phương trình tuyến tính lớn. Bất kể bạn xếp chồng bao nhiêu lớp, đầu ra vẫn là một hàm tuyến tính của đầu vào.

Các hàm kích hoạt giới thiệu tính phi tuyến, cho phép mạng xấp xỉ các hàm phức tạp như:

  • Nhận diện hình ảnh
  • Xử lý ngôn ngữ tự nhiên
  • Học tăng cường

Về mặt toán học, một hàm kích hoạt ( f(x) ) biến đổi đầu ra của mỗi nơ-ron trước khi truyền nó đến lớp tiếp theo.

🔢 Các hàm kích hoạt phổ biến

Hãy cùng đi qua các hàm kích hoạt phổ biến nhất, công thức, trường hợp sử dụng và hạn chế của chúng.

1️⃣ Sigmoid

f(x)=11+e−xf(x) = \frac{1}{1 + e^{-x}}
  • Phạm vi: (0, 1)
  • Trường hợp sử dụng: Phân loại nhị phân (hồi quy logistic)
  • Nhược điểm: Bão hòa với ∣x∣|x| lớn, gây ra gradient biến mất

2️⃣ Tanh

f(x)=tanh⁡(x)=ex−e−xex+e−xf(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
  • Phạm vi: (-1, 1)
  • Trường hợp sử dụng: Thường được ưa thích hơn sigmoid trong các lớp ẩn
  • Nhược điểm: Vẫn gặp vấn đề gradient biến mất

3️⃣ ReLU (Rectified Linear Unit)

f(x)=max⁡(0,x)f(x) = \max(0, x)
  • Phạm vi: [0, ∞)
  • Trường hợp sử dụng: Lựa chọn mặc định cho các lớp ẩn trong CNN và MLP
  • Ưu điểm: Hiệu quả tính toán, kích hoạt thưa thớt
  • Nhược điểm: Vấn đề ReLU chết - các nơ-ron có thể xuất ra số không vĩnh viễn

4️⃣ Leaky ReLU

f(x)={xextifx≥0αxextifx<0f(x) = \begin{cases} x & ext{if } x \geq 0 \alpha x & ext{if } x < 0 \end{cases}
  • Khắc phục vấn đề nơ-ron chết của ReLU bằng cách cho phép một độ dốc nhỏ trong vùng âm (α≈0.01\alpha \approx 0.01)

5️⃣ GELU (Gaussian Error Linear Unit)

f(x)=x⋅Φ(x)f(x) = x \cdot \Phi(x)

Trong đó Φ(x)\Phi(x) là hàm phân phối tích lũy của phân phối chuẩn tiêu chuẩn.

  • Trường hợp sử dụng: Transformer (ví dụ: BERT, GPT)
  • Ưu điểm: Mượt mà và có thể vi phân; hoạt động tốt trong LLM lớn

📊 So sánh trực quan các hàm kích hoạt

So sánh trực quan các hàm kích hoạt

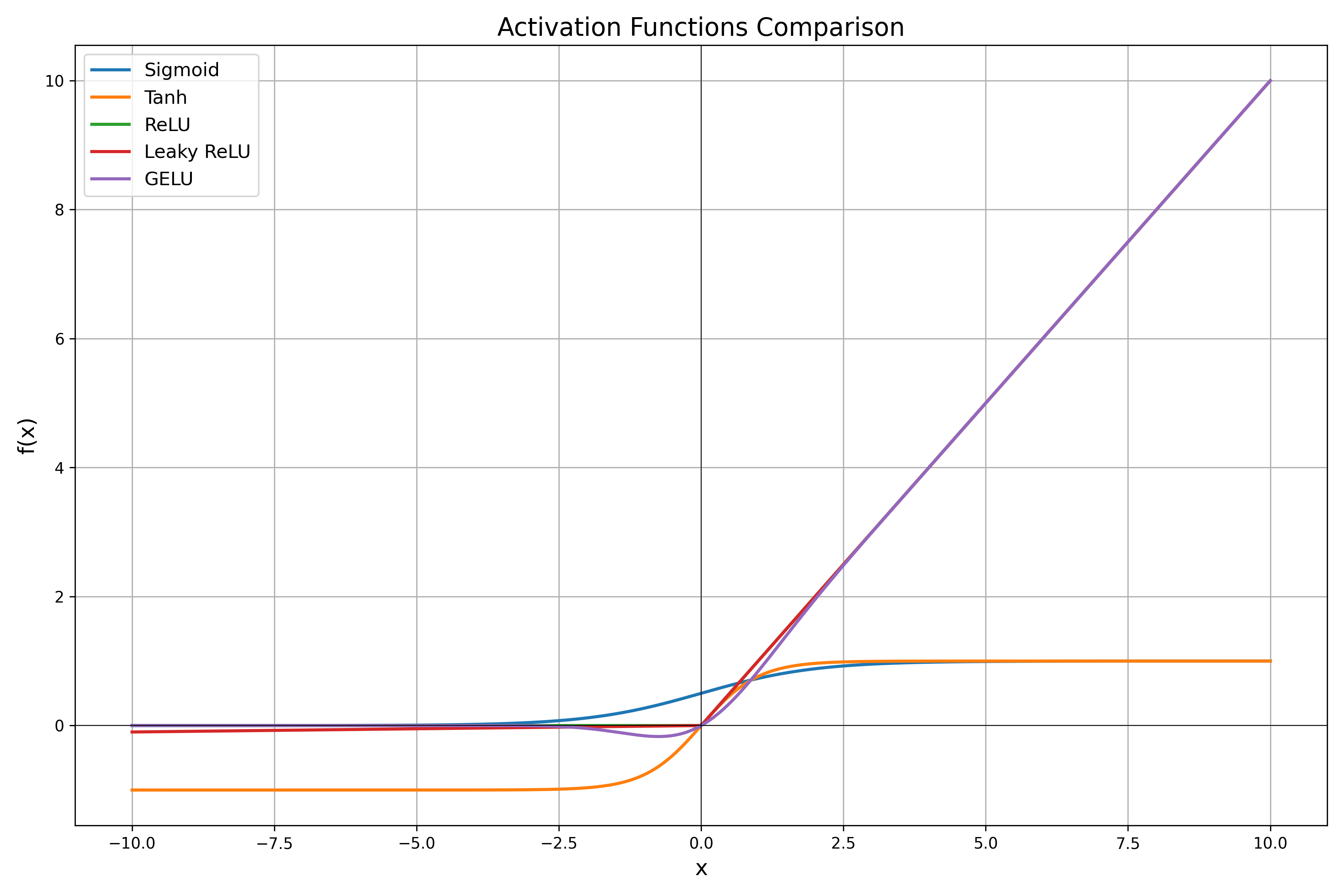
🙏 Lời cảm ơn

Cảm ơn ChatGPT đã cải thiện bài viết này với các gợi ý, định dạng và biểu tượng cảm xúc.